Геометрические фракталы
Из геометрических фракталов очень интересным и довольно знаменитым является фрактал "Снежинка Коха". Строится она на основе равностороннего треугольника.
Пусть сторона исходного треугольника равна 1. Его площадь также равна 1.
Основными представителями этой группы фракталов являются такие объекты, как: кривая Пеано, снежинка Коха, треугольник
Серпинского, пыль Кантора, «дракон» Хартера-Хейтуэя..[2]. Все они получены
путем повторений определенной последовательности геометрических построений с
использованием точек и линий. Кантор с помощью простой рекурсивной процедуры
«превратил» линию в набор несвязных точек: брал линию и выносил её центральную
треть на определенное расстояние, затем повторял эту процедуру с остальными
отрезками. Джузеппе Пеано нарисовал особую линию, используя довольно простой
алгоритм: он брал прямую линию, затем заменял её девятью отрезками, каждый из
которых затем вновь подвергал этой процедуре и т.д.
Фракталы этой группы самые
наглядные. Если проанализировать данные изображения, можно выделить следующие
свойства геометрических фракталов:
Снежинка Коха
Из геометрических фракталов очень интересным и довольно знаменитым является фрактал "Снежинка Коха". Строится она на основе равностороннего треугольника.
Пусть сторона исходного треугольника равна 1. Его площадь также равна 1.
Каждая сторона делится на три части каждая длиной в 1/3 исходной стороны. Затем пририсовывются три меньших равносторонних треугольника по одному на каждой стороне (на стредней трети). На каждой из полученных 12 сторон пририсовываются по одному ещё меньшему треугольнику (снова на средней трети стороны).
Таким образом, с каждой итерацией длина кривой увеличивается на треть.
Этот процесс можно продолжать бесконечно долго.
Каждый раз число сторон учетверяется. Число сторон можно выразить такой последовательностью:
3, 3*4, 3*4*4, 3* 4*4*4, 3* 4*4*4*4....
Убеждаемся, что число сторон снежинки бесконечно велико.
Снежинка образуется добавлением треугольника к каждой стороне, так что выписанная последовательность даёт иакже и число треугольников, добавляемое на каждом этапе (каждой итерации). Начиная со второго этапа, количество добавляемых треугольников каждый раз учетверяется.
Общую площадь снежинки можно выразить геометрическим рядом
1+ 1/3 + (1/3) * (4/9) + (1/3) * (4/9)*(4/9) + (1/3) * (4/9)*(4/9)*(4/9) + ...
Сумма этого ряда конечна и равна 1,6.
Треугольник Серпинского (http://elementy.ru/posters/fractals/Sierpinski)
Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.
Выкидывание центральных треугольников — не единственный способ получить в итоге треугольник Серпинского. Можно двигаться «в обратном направлении»: взять изначально «пустой» треугольник, затем достроить в нём треугольник, образованный средними линиями, затем в каждом из трех угловых треугольников сделать то же самое, и т. д. Поначалу фигуры будут сильно отличаться, но с ростом номера итерации они будут всё больше походить друг на друга, а в пределе совпадут.
Алгебраические фракталы
Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится, на экран выводится точка.
Сумма этого ряда конечна и равна 1,6.
При этом периметр снежинки, напротив, бесконечен.
Треугольник Серпинского (http://elementy.ru/posters/fractals/Sierpinski)
Этот фрактал описал в 1915 году польский математик Вацлав Серпинский. Чтобы его получить, нужно взять (равносторонний) треугольник с внутренностью, провести в нём средние линии и выкинуть центральный из четырех образовавшихся маленьких треугольников. Дальше эти же действия нужно повторить с каждым из оставшихся трех треугольников, и т. д. На рисунке показаны первые три шага, а на флэш-демонстрации вы можете потренироваться и получить шаги вплоть до десятого.
|
|
Алгебраические фракталы
Вторая большая группа фракталов - алгебраические. Свое название они получили за то, что их строят, на основе алгебраических формул иногда весьма простых. Методов получения алгебраических фракталов несколько. Один из методов представляет собой многократный (итерационный) расчет функции Zn+1=f(Zn), где Z - комплексное число, а f некая функция. Расчет данной функции продолжается до выполнения определенного условия. И когда это условие выполнится, на экран выводится точка.
При этом значения функции для разных точек комплексной плоскости может иметь разное поведение:
К алгебраическим фракталам относят фракталы Фату.
Фату изучал рекурсивные процессы вида
Множество Мандельброта
Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение. Эти феномены рождались при использовании рекурсивного алгоритма для получения какой-либо кривой или множества. Множество Мандельброта — один из таких феноменов, названный по имени своего исследователя. Википедия
Множество Мандельброта — классический образец фрактала.
Множество Мандельброта — это множество таких точек С на комплексной плоскости:
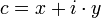
Z0 = 0
- С течением времени стремится к бесконечности.
- Стремится к нулю.
- Принимает несколько фиксированных значений и не выходит за их пределы.
- Поведение хаотично, без каких либо тенденций.
К алгебраическим фракталам относят фракталы Фату.
Фату изучал рекурсивные процессы вида
Начав с точки  на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу.
на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу.
Такая последовательность точек называется орбитой при преобразовании
при преобразовании 
 на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу.
на комплексной плоскости, можно получить новые точки, последовательно применяя к ним эту формулу. Такая последовательность точек называется орбитой
 при преобразовании
при преобразовании 
Фату нашел, что орбита  при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований — своё для каждого значения
при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований — своё для каждого значения  . В те времена компьютеров ещё не было, и Фату, конечно, не мог построить орбиты всех точек плоскости, ему приходилось всё делать вручную. Основываясь на своих расчётах, он доказал, что орбита точки, лежащей на расстоянии больше 2 от начала координат, всегда уходит в бесконечность.
. В те времена компьютеров ещё не было, и Фату, конечно, не мог построить орбиты всех точек плоскости, ему приходилось всё делать вручную. Основываясь на своих расчётах, он доказал, что орбита точки, лежащей на расстоянии больше 2 от начала координат, всегда уходит в бесконечность.
 при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований — своё для каждого значения
при этом преобразовании показывает достаточно сложное и интересное поведение. Существует бесконечное множество таких преобразований — своё для каждого значения  . В те времена компьютеров ещё не было, и Фату, конечно, не мог построить орбиты всех точек плоскости, ему приходилось всё делать вручную. Основываясь на своих расчётах, он доказал, что орбита точки, лежащей на расстоянии больше 2 от начала координат, всегда уходит в бесконечность.
. В те времена компьютеров ещё не было, и Фату, конечно, не мог построить орбиты всех точек плоскости, ему приходилось всё делать вручную. Основываясь на своих расчётах, он доказал, что орбита точки, лежащей на расстоянии больше 2 от начала координат, всегда уходит в бесконечность.
Фату никогда не видел изображений, которые мы сейчас знаем как изображения множества Мандельброта, потому что необходимое количество вычислений невозможно провести вручную.
Первым, кто применил компьютер лдля расчёта фракталов на комплексной плоскости, стал Бенуа Мандельброт. Благодаря этому он впервые открыл нам красоту фракталов.
Первым, кто применил компьютер лдля расчёта фракталов на комплексной плоскости, стал Бенуа Мандельброт. Благодаря этому он впервые открыл нам красоту фракталов.
Множество Мандельброта
Фракталы были описаны Мандельбротом в 1975 году в его книге «Les Objets Fractals: Forme, Hasard et Dimension» («Фрактальные объекты: форма, случайность и размерность»). В этой книге Мандельброт впервые использовал термин «фрактал» для обозначения математического феномена, демонстрирующего столь непредсказуемое и удивительное поведение. Эти феномены рождались при использовании рекурсивного алгоритма для получения какой-либо кривой или множества. Множество Мандельброта — один из таких феноменов, названный по имени своего исследователя. Википедия
Множество Мандельброта — это множество таких точек С на комплексной плоскости:
Z0 = 0
Функционально множество Мандельброта определяется как Zn+1=Zn*Zn+C.
Для всех точек на комплексной плоскости в интервале от -2+2i до 2+2i выполняем некоторое достаточно большое количество раз это выражение и каждый раз проверяя абсолютное значение Zn. Если это значение больше 2, что рисуем точку с цветом равным номеру итерации на котором абсолютное значение превысило 2, иначе рисуем точку черного цвета. Все множество Мандя коллекция ельброта в полной красе у нас перед глазами.
Черный цвет в середине показывает, что в этих точках функция стремится к нулю - это и есть множество Мандельброта. За пределами этого множества функция стремится к бесконечности. А самое интересное это границы множества. Они-то и являются фрактальными. На границах этого множества ведет себя непредсказуемо - хаотично.
На странице "Программирование фракталов" нашего блога представлена программа расчёта множества Мандельброта на языке Small Basic.
Алгебраические фракталы воодушквили компьютерных художников на создание фрактальных композиций удивительной красоты. В этих комозициях можно найти сходство с природными фракиалами и проявление творческой фантазии художников.
На сайте http://www.fractalartcontests.com/2011/ собрана богатейшая коллекция очень красивых фрактальных композиций. Вот некоторые из них:
Алгебраические фракталы воодушквили компьютерных художников на создание фрактальных композиций удивительной красоты. В этих комозициях можно найти сходство с природными фракиалами и проявление творческой фантазии художников.
На сайте http://www.fractalartcontests.com/2011/ собрана богатейшая коллекция очень красивых фрактальных композиций. Вот некоторые из них:
A Sunny Day for Vincent (Солнечный день Винсента)
Daisies and Blue Sky (Маргаритка и синее небо)
Autumn (Осень)
Cockatoo (Какаду)









обратись к моему однокласснику))
ОтветитьУдалитьлучшие тусовки у меня в школе
Удалить